.:: RaopNet 2.0 ::.: Qué es y de dónde proviene el número áureo

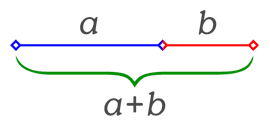
Se divide un segmento cualquiera en dos partes de forma que la razón entre la totalidad del segmento y una parte (la mayor) sea igual a la razón entre esta parte y la otra. Matemáticamente, siendo las partes a y b :

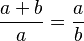
$\frac{a + b}{a} = \frac{a}{b}$

Esta relación cumple la propiedad denominada razón áurea.

Para obtener el valor de $\varphi$ a partir de esta razón considere lo siguiente:

Que la longitud del segmento más corto b sea 1 y que la de a sea x. Para que estos segmetos cumplan con la razón áurea la razón los segmentos a y b deben cumplir que:

$\frac{x + 1}{x} = \frac{x}{1}$

Multiplicando ambos lados por x y reordenando:

$\ x^2 - x -1 = 0$

Se puede despejar x utilizando la fórmula general de las ecuaciones de segundo grado. Las dos soluciones de la ecuación son

$x = \frac{1 + \sqrt{5}}{2}$

$x = \frac{1 - \sqrt{5}}{2}$

La solución positiva es el valor del número áureo, y esto es una prueba formal de que el número áureo es irracional, ya que incluye un la raíz de un número primo.

La solución negativa en cambio, es igual a:

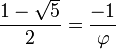
$\frac{1 - \sqrt{5}}{2} = \frac{-1}{\varphi}$

El rectángulo áureo de Euclides

Euclides obtiene el rectángulo áureo AEFD a partir del cuadrado ABCD. El rectángulo BEFC es asimismo áureo.

El rectángulo AEFD es áureo porque sus lados AE y AD están en la proporción del número áureo. Euclides en su proposición 2.11 de Los elementos obtiene su construcción.>

$GC = \sqrt{5}$

Con centro en G se obtiene el punto E, y por lo tanto

$GE=GC=\sqrt{5}$

resultando evidente que

$AE = AG + GE = 1 + \sqrt{5}$

de donde, finalmente

$\frac{AE}{AD} = \frac{1 + \sqrt{5}}{2}= \varphi$

Por otra parte, los rectángulos AEFD y BEFC son semejantes, de modo que éste último es asimismo un rectángulo áureo.

Propiedades

Φ es irracional, y el único número real positivo con:

$\varphi^2 = \varphi + 1\$

La expresión anterior es fácil de comprobar:

$\varphi^2 = \frac{1 + 2\sqrt{5} + 5}{2^2} = \frac{6 + 2\sqrt{5}}{2^2} = \frac{3 + \sqrt{5}}{2}$

$\varphi + 1 = \frac{1 + \sqrt{5}}{2} + \frac{2}{2} = \frac{3 + \sqrt{5}}{2}$

Φ posee además las siguientes propiedades:

$\varphi - 1 = \frac{1}{\varphi} \$

$\varphi^3 = \frac {\varphi + 1} {{\varphi - 1}} \$

Representación mediante fracciones continuas

La expresión mediante fracciones continuas es:

$\varphi = 1 + \frac{1}{\varphi} \quad \longrightarrow \quad \varphi = 1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{1 + ...}}}}$

Sorprendente interacción única (suma y multiplicación), (resta y división), donde sumar es multiplicar y restar es dividir.

El doctor Tobías Dantzig, en vida profesor emérito de la Universidad de Columbia, sugirió que esta expresión en fracción continua en la que solamente aparece la unidad podría justificar el nombre de "divina proporción".

Las fracciones continuas son conocidas desde la Antigüedad y aparecen en el Libro VIII de los Elementos de Euclides, Alejandría, siglo 3 a.E.C. Su estudio continuó a partir de 1572 en un trabajo de Rafael Bombelli.

Para la geometría sagrada de los sacerdotes paganos los únicos números bona fide eran los enteros a partir del número 1; pero este número no era considerado como tal, sino el origen de todo y la divinidad antes del acto de creación. Esta filosofía consideraba que lo visible se generaba en la disección o dualidad creadora, en la división de la unidad en dos partes opuestas, como luz-oscuridad, masculino-femenino, fijo-volátil, etc. Para ellos el primer número era 2, considerado femenino al igual que todos los números pares. La Geometría era considerada superior a la Aritmética y los números solían representarse por segmentos de recta.

Representación mediante ecuaciones algebraicas

$(\varphi)(\varphi - 1) = 1 \quad \longrightarrow \quad (\varphi)^2 - \varphi - 1 = 0 \quad \longrightarrow \quad \varphi = \frac{1 + \sqrt{5}}{2}$

El número áureo 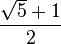$\frac{\sqrt{5} + 1}{2}$ y la sección áurea 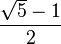$\frac{\sqrt{5} - 1}{2}$ son soluciones de las siguientes ecuaciones:

$\ x^2 - \sqrt{5}\, x + 1 = 0$

$\ x^3 - y^3 - 4 = 0$

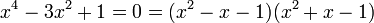
$\ x^4 - 3 x^2 + 1 = 0 = (x^2 - x - 1) (x^2 + x - 1)$

Representación trigonométrica

$\varphi = \frac{1}{2} sec \frac{2}{5} \, \pi \$

Representación mediante raíces anidadas

$\varphi = \sqrt{1 + \varphi} \quad \longrightarrow \quad \varphi = \sqrt{1 + \sqrt{1 + \sqrt{1 + \sqrt{1 +\cdots }}}}$

Esta fórmula como caso particular de una identidad general publicada por Nathan Altshiller-Court, de la Universidad de Oklahoma, en la revista American Mathematical Monthly, 1917.

El teorema general dice:

La expresión 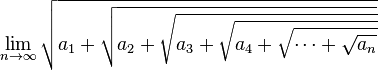$\lim_{n \to \infty} \sqrt{a_1 + \sqrt{a_2 + \sqrt{a_3 + \sqrt{a_4 +\sqrt{\cdots + \sqrt{a_n}}}}}}$ (donde $a i = a$ ), es igual a la mayor de las raíces de la ecuación x² - x - a = 0; o sea, $\frac {1 + \sqrt{1 + 4a}}{2}$

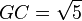
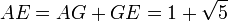
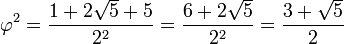
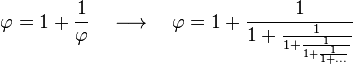
1 comentario:

Anónimo dijo...: [url=http://www.ganar-dinero-ya.com][img]http://www.ganar-dinero-ya.com/ganardinero.jpg[/img][/url]
[b]Estas buscando formas de ganar dinero[/b]
Nosotros hemos hallado la mejor guia en internet de como trabajo casa. Como fue de interes para nosotros, tambien les puede ser de interes para ustedes. No son unicamente metodos de ganar dinero con su pagina web, hay todo tipo de metodos para ganar dinero en internet...
[b][url=http://www.ganar-dinero-ya.com][img]http://www.ganar-dinero-ya.com/dinero.jpg[/img][/url]Te recomendamos entrar a [url=http://www.ganar-dinero-ya.com/]Ganar dinero desde casa[/url][url=http://www.ganar-dinero-ya.com][img]http://www.ganar-dinero-ya.com/dinero.jpg[/img][/url][/b]; jue feb 18, 04:32:00 p. m. 2010